3. Modelling the cost
Look at the following graph:
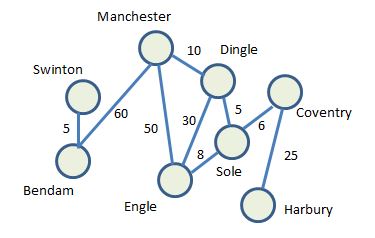
Any non-trivial path needs to define three things - a start node, a target node and an intermediate node designated $n$ if there isn't a direct edge between start and target.
As a path is built up, an estimate of the cost so far, can be expressed with
$f(n) = g(n) + h(n)$
where $f(n)$ is the total estimated cost of getting to the target from node $n$. It is in two parts $g(n)$ is the actual cost so far of getting to $n$ and $h(n)$ is an estimate of the further cost needed to get to the goal.
The name given to $h(n)$ is the heuristic function.
The role of a shortest path algorithm is to find the path with the minimum $f(n)$ with $n$ being the target.
Some algorithms do not use a guess, in which case $h(n)$ remains zero, for example the Dijkstra algorithm which we will be describing does not try to make a guess, but relies on the actual costs found so far.
Selecting a suitable heuristic function depends on the nature of the problem.
For example, if a path-finding program is trying to work out a flight schedule for an aircraft, a good heuristic is to work out the Great Circle distance from a way point to the destination as that is the most direct route. This is a good heuristic because: (1) the maths is easily worked out (2) it is guaranteed to be a good estimate as that would be the ideal solution if the plane were allowed to fly it. (Often they are not allowed because all countries have very specific paths that aircraft can use).
If the problem is to find the shortest path between two points in a 2D grid, then a good heuristic is to just add the horizontal and vertical units from the current point to the target. The distance from green to red is 3 units horizontal and 4 units vertical, so the heuristic is 7 units.
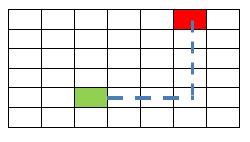
This is sometimes called the Manhattan heuristic as that city is built in a grid format.
An alternative is to calculate the hypotenuse of the two points as that is the shortest distance.
But that heuristic is only relevant if that path is allowed in the first place.
So path-finding algorithms depend to some extent on the constraints which limit the paths available.
Challenge see if you can find out one extra fact on this topic that we haven't already told you
Click on this link: Modelling graph cost functions
