1. Introduction to Karnaugh Maps
There are often multiple ways of writing the same equation.
For example, a maths problem written as
$$AB = A(C+D)$$
can be simplified by dividing both sides by A, producing
$$B = C + D$$
The same is true of Boolean equations, too. For example,
$$Q = A.B + \overline{(C+A+F)} + \overline B + C$$
This uses a lot of logic gates, and overall seems very complicated. But how do you simplify Boolean equations?
This is where karnaugh maps come in (pronounced 'carno'). They are a visual way of simplifying a boolean expression, letting you use as few gates as possible to produce a particular function
This is what a Karnaugh map looks like
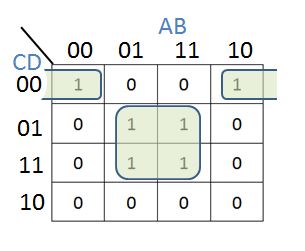
In this section, we'll show you how to both build and use karnaugh maps.
Challenge see if you can find out one extra fact on this topic that we haven't already told you
Click on this link: What is a karnaugh map
