3. Karnaugh map grid

From the previous page, this is the expression we want to simplify

$$Q = \overline A. \overline B.C. \overline D + \overline A. \overline B.C.D + \overline A.B.C. \overline D + \overline A.B.C.D + A. \overline B. \overline C. \overline D + A.B. \overline C. \overline D + A.B. \overline C.D $$

This is done with the following steps:

1. Create a grid for the karnaugh map
2. Fill in the '1's in the appropriate places
3. Split the map up into regions
4. Create minterms for each region
5. Combine the minterms

Step 1: Creating the grid

Karnaugh maps are two-dimensional. So with four inputs, the first step is to combine them together to fit onto two axes. We'll pair up A and B to produce AB for one axis. And we'll pair C and D to produce CD for the other axis.

The next step is to label each row and column. A can only be 0 or 1, and B can only be 0 or 1, so there are four possible values for AB - 00, 01, 10, and 11. The same is true for the pair CD.

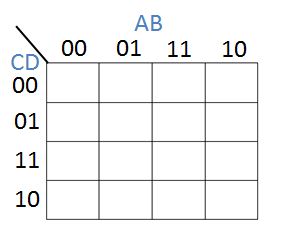
An important thing to notice is the sequence of AB (same for CD) - only one bit it allowed to change as you go from one state to another. For example this sequence is NOT correct: 00,01,10,11 because two bits changed to go from 01 to 10. A binary sequence where only one bit changes along the sequence is called a gray code after Frank Gray. Karnaugh maps use gray code to determine the rows and columns.

So what do these cells actually represent? Let's look at the top left cell:

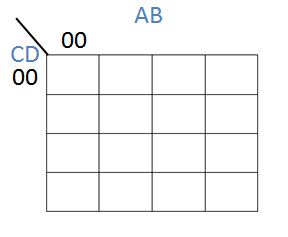
In this cell, the result is not-A AND not-B AND not-C AND not-D. Or, in Boolean algebra, $\overline A. \overline B. \overline C. \overline D$, with a top bar representing NOT and a dot representing the AND operator.

The next pair of cells represent expressions with a single True value - either B or D:

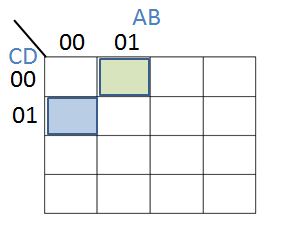
The green cell represents $\overline A. B. \overline C. \overline D$ and the blue cell represents $\overline A. \overline B. \overline C.D$

Next, place a 11 alongside:

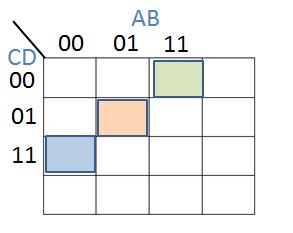
The green cell is $A.B. \overline C. \overline D$, the orange cell is $\overline A.B. \overline C.D$ and the blue cell is $\overline A. \overline B.C.D$

Now finally place a 10 next to the 11:

This is the empty four-variable karnaugh map. Because there are 16 cells, every possible combination of $A,B,C,D$ can be defined.

It is important to note that this is a representation of logic, rather than binary arithmetic. Unlike binary arithmetic, where 00 and 10 represent 0 and 2 the sequence 00 means two inputs with each at state 0.

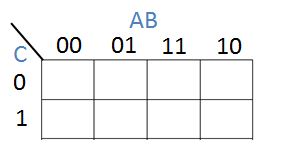
An empty karnaugh map for three variables would look like this: